El calentamiento global es uno de los grandes desafíos de nuestro siglo. Es un problema amplio y complejo que requiere ser analizado desde diversas perspectivas; una de ellas, quizás no tan conocida, es el estudio de los remolinos oceánicos. El incremento de estos remolinos es uno de los muchos síntomas de la subida de temperaturas del planeta. Pero, además, este fenómeno afecta al clima, por lo que entender sus mecanismos de formación y evolución es fundamental para estudiar el cambio climático. Las matemáticas nos ofrecen herramientas para hacerlo.

Una de las características más interesantes de los remolinos marinos, que es un fenómeno mucho menos popular que el de los huracanes o el de los tornados atmosféricos, es que no dejan salir lo que se encuentra en su interior, como un agujero negro. Así, el agua que capturan (que tiene propiedades físicas, químicas y biológicas peculiares y puede incluir cuerpos extraños como plástico y manchas de petróleo) es transportada durante varios meses a lo largo de distancias de miles de kilómetros. En este sentido, actúan como taxis marinos, que permiten conectar áreas del océano independientes entre sí, modificando la dinámica oceánica y el clima.

Para detectar los remolinos en el océano se analizan las corrientes. Es decir, la velocidad del fluido en cada punto. Efectivamente, los remolinos se forman por diferentes mecanismos, pero el más habitual es cuando las corrientes se doblan, haciendo “bucles”. En estos torcimientos, la corriente se cierra sobre sí misma, formando un círculo que se desprende. Monitorizar y describir estas corrientes es crucial para predecir la aparición de remolinos y estudiar su evolución.

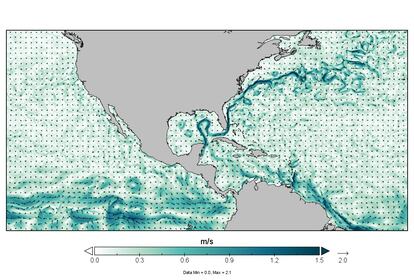
Uno de los métodos para ello consiste en emplear datos de satélite, que permiten calcular las corrientes. Atendiendo a los datos de velocidad del agua (representados en la figura 1 con flechas negras), es fácil intuir una zona de remolino: será donde las flechas forman una trayectoria circular. En términos matemáticos, las flechas representan un campo vectorial, a partir del cual se pueden calcular parámetros físicos del remolino, como la llamada vorticidad, que permiten describir el fenómeno y hacer predicciones sobre su evolución.

La vorticidad refleja, en cada punto, un cambio de la velocidad en la dirección horizontal y vertical del mapa. Dicho en otras palabras, es una medida de cuánto se tuerce la corriente en cada punto. En la figura 2, los tonos de color azul y rojo corresponden a valores de vorticidad. Cuando el remolino tiene vorticidad positiva (en la imagen, representado con el tono verde) gira en sentido contrario a las manecillas del reloj, mientras que cuando tienen vorticidad negativa (tono rojo), lo hace al revés.

Sin embargo, no siempre es sencillo detectar a simple vista un remolino y seguir su evolución. Para esto, se están desarrollando nuevas técnicas, propias de la teoría de los sistemas dinámicos, como los llamados descriptores lagrangianos. Estas herramientas ofrecen un análisis más sofisticado de las corrientes, ya que permiten observar estructuras geométricas subyacentes en el movimiento del océano. Procesando los datos usando con esta técnica es posible visualizar de forma mucho más precisa los bordes y forma de los remolinos.

Además, al aplicar los descriptores lagrangianos de forma masiva se obtienen bases de datos de la localización, tamaño y evolución de los remolinos a lo largo de los años. Esta información es muy relevante para entender como están cambiando los océanos. En concreto, se podría usar para obtener mejores predicciones del crecimiento del nivel del mar en los siguientes años y mitigar el impacto de posibles inundaciones.

Este es solo un ejemplo de la importancia de describir y comprender correctamente los remolinos. Es un tema muy complejo que necesita de la colaboración de diferentes campos de la ciencia como la oceanografía, climatología, mecánica de fluidos y otras ramas de las matemáticas, y que permitirá avanzar en el desafío del cambio climático.

Fuente:https://elpais.com/ciencia/cafe-y-teoremas/2022-06-23/matematicas-para-describir-los-remolinos-los-taxis-del-oceano.html