
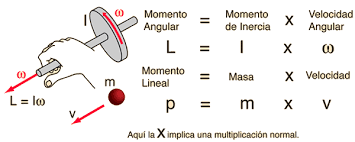
Las magnitudes que se miden en el momento angular son el momento de inercia y la velocidad angular
Para explicar lo que es el momento angular voy a relacionarlo con el momento lineal porque la mayoría estamos mucho más acostumbrados a pensar en este. Si queremos caracterizar el movimiento de un cuerpo, necesitamos dos cantidades: la masa y la velocidad. Es fácil entenderlo de forma intuitiva: no es lo mismo que algo muy ligero, una hoja de un árbol, se mueva hacia nosotros, que lo haga algo muy pesado, un ladrillo.
Y de igual forma, si esos dos objetos se mueven hacia nosotros, nos interesa saber si se mueven rápido o despacio. Así que podemos entender que nos hacen falta las dos magnitudes para medir esa cantidad de momento lineal. Cuando algo gira, cuando tiene un movimiento de rotación en torno a un eje o a un punto de referencia, utilizamos el momento angular en vez del momento lineal del que acabo de hablar.
Es decir, el momento angular con respecto a un punto caracteriza el movimiento de algo que rota en torno a ese mismo punto. En este caso, las dos magnitudes que necesitamos para medirlo son el momento de inercia (lo que en el lineal es la masa) y la velocidad angular (lo que en el lineal es la velocidad lineal).
El momento angular no es una característica intrínseca de un cuerpo. La masa, por ejemplo, sí lo es, cada cuerpo tiene su masa. El momento angular se define siempre con respecto a un punto que será el centro de rotación. Por eso, un objeto puede tener un momento angular determinado con respecto a un punto, pero no tenerlo con respecto a otro. Lógicamente, solo cuando gira y siempre con respecto al punto de rotación. Es como la velocidad, algo se está moviendo o no, con respecto a qué lo midamos. Si yo conduzco un coche con un copiloto, alguien que nos vea pasar ve cómo mi copiloto se mueve, pero para mí no se está moviendo porque va sentado a mi lado.
Otro hecho interesante del momento angular es que se conserva, es decir, que el momento angular de un cuerpo con respecto a un punto no va a cambiar, a no ser que se aplique una fuerza externa. Y no vale cualquier fuerza, tiene ser una que cambie el estado de rotación del objeto.
Podemos pensar en dos casos con dos tipos de fuerzas, una que no cambie el momento angular y otra que sí lo haga. Por ejemplo, en un sistema planetario los planetas giran en torno a un punto y tienen un momento angular que se mantendrá mayoritariamente constante. Esto se cumple porque la fuerza de la gravedad que actúa sobre ellos es central, así que no cambia su velocidad de rotación en torno a ese punto central. Para el segundo caso, si pensamos en una rueda de bicicleta girando y queremos hacer que gire más rápido, la vamos a impulsar tangencialmente (y no hacia el centro de la rueda, que es donde está el eje de giro). Como el momento angular se calcula como el producto del momento de inercia y la velocidad angular, vemos que al cambiar la velocidad de giro con una fuerza tangencial también estamos cambiando el momento angular de la rueda.
Finalmente, nos queda hablar sobre el momento de inercia. Esta cantidad nos dice para un determinado cuerpo cómo se distribuyen todas las partes que lo componen con respecto a un eje de rotación. Es decir, si la masa del objeto que gira está cerca o lejos del eje. Cuanto mayor sea la distancia al eje de rotación, mayor será el momento de inercia correspondiente. Como el momento angular, no es algo intrínseco, y es que el momento de inercia de un cuerpo cambiará si cambia su forma o si cambiamos el eje de rotación.
Hay un ejemplo que nos sirve para ilustrarlo y es el patinaje artístico. En este deporte vemos como cambiando la posición del cuerpo, si se acerca o se aleja una parte del cuerpo al centro de giro durante una pirueta, cambia la velocidad de giro del atleta. Lo que estamos viendo es que su momento angular se mantiene constante durante la pirueta porque el efecto total de las fuerzas externas es muy pequeño y podemos ignorarlo. Como el momento angular es el producto de esas dos cantidades de las que hablaba, momento de inercia y velocidad angular, si una disminuye, la otra tiene que aumentar. Al acercar brazos y piernas al eje de giro, el momento de inercia disminuye, así que la velocidad de giro tiene que aumentar para el que el producto de las dos, es decir, el momento angular, se mantenga constante.
María Vieites Díaz es doctora en Física de Partículas e investigadora en el Laboratorio de Física de Altas Energías de la Escuela Politécnica Federal de Lausana (Suiza).
Fuente:https://elpais.com/ciencia/las-cientificas-responden/2022-04-29/que-es-el-momento-angular.html

Sé el primero en comentar en «¿Qué es el momento angular?»