 En la fachada principal de la Catedral de Notre Dame (París, Francia) hay varios rectángulos dorados.
En la fachada principal de la Catedral de Notre Dame (París, Francia) hay varios rectángulos dorados.
El rectángulo de 2 x 1, llámese dominó o tatami, no es el único especial: hay al menos otros dos rectángulos singulares
Hemos visto, en las semanas anteriores, algunas de las posibilidades del rectángulo de 2 x 1 como tesela, tatami o ladrillo, que lo convierten, seguramente, en el más “popular” y difundido de los rectángulos. Pero hay al menos otros dos rectángulos especiales que encontramos a menudo a nuestro alrededor.
Pero el más notable, si no el más popular, de los rectángulos es el que cumple la propiedad que ilustra la figura adjunta: si a partir de un vértice llevamos el lado menor sobre el mayor y, levantando una perpendicular desde su extremo, formamos un cuadrado, el rectángulo menor resultante es proporcional al rectángulo mayor. Si el lado menor mide 1, ¿cuánto mide el mayor?

Es el famoso rectángulo áureo o rectángulo dorado, que ya los antiguos griegos tomaron como referente estético para sus construcciones y obras de arte (lo encontramos, por ejemplo, en la fachada del Partenón). Los arquitectos y artistas plásticos del Renacimiento lo recuperaron y utilizaron profusamente (es fácil descubrirlo, por ejemplo, en las composiciones pictóricas de Leonardo), y sigue siendo un referente estético imprescindible en la actualidad. También en la fachada de la catedral de Notre Dame, que hace exactamente un año sufrió un terrible incendio, encontramos varios rectángulos dorados, ¿los distingues?
¿Podrías construir un rectángulo áureo con regla (no graduada) y compás?
Pero ¿por qué precisamente esta proporción nos parece tan bella? La relación entre los lados del rectángulo áureo no es un número entero, ni siquiera racional, por lo que los pitagóricos se resistieron a aceptar este modelo. Y sin embargo se impuso, y para siempre. ¿Dónde reside su recóndita armonía?
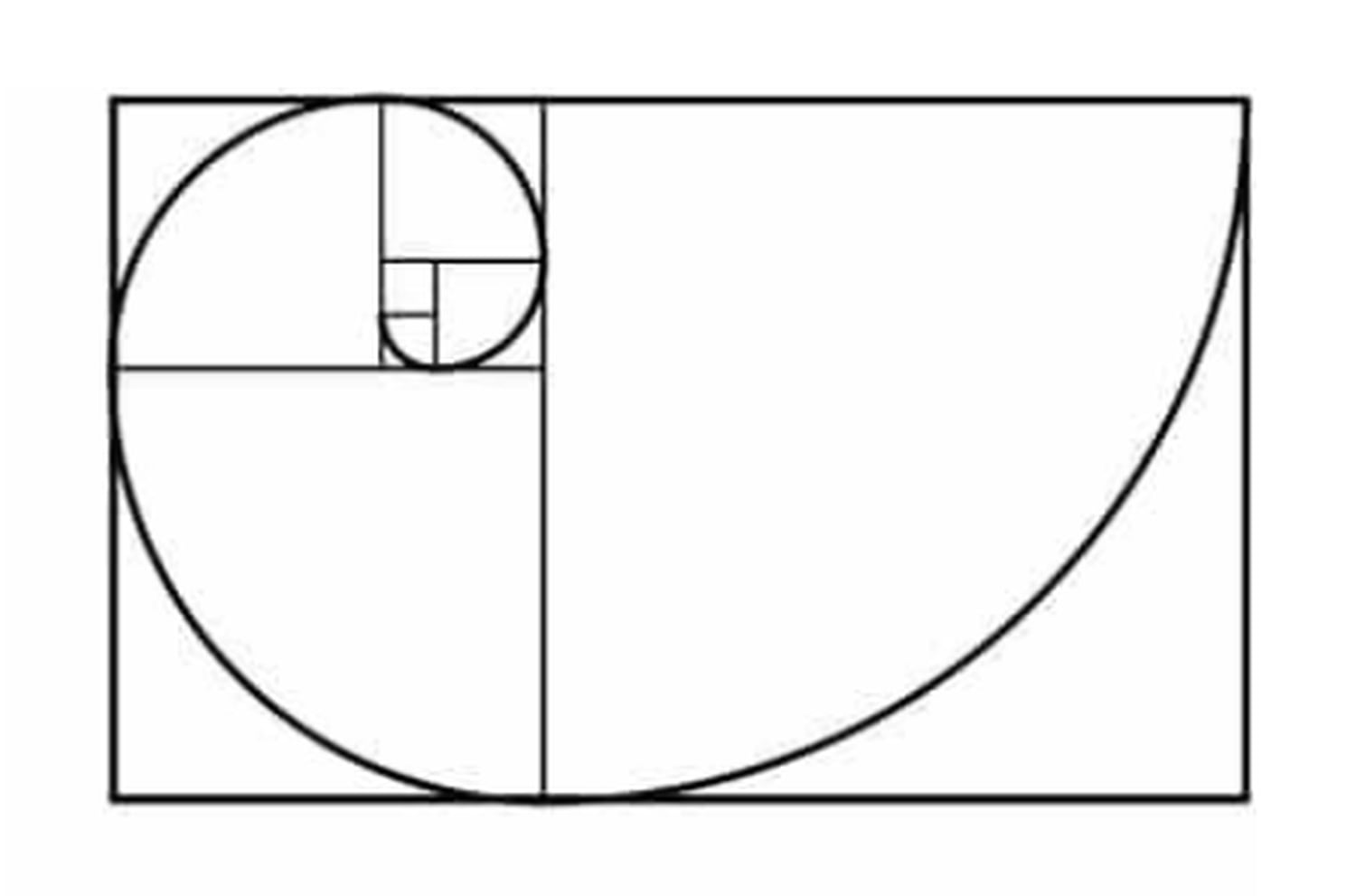
Puesto que el rectángulo menor de la figura anterior es semejante al mayor, también es áureo, y podemos repetir con él la operación, y también con el siguiente, y así sucesiva e indefinidamente. Y si en cada uno de los sucesivos cuadrados resultantes trazamos un cuadrante de circunferencia, obtenemos una espiral dorada, también conocida como espiral de Durero, que es una buena aproximación a un espiral equiangular (aquella en la que el ángulo que forman el radio vector y la tangente es constante).
Y del cuadrado duplicado del rectángulo de 2 x 1, a un fantasmal cuadrado demediado: el de la figura adjunta, enviada por Carlos Gaceo.
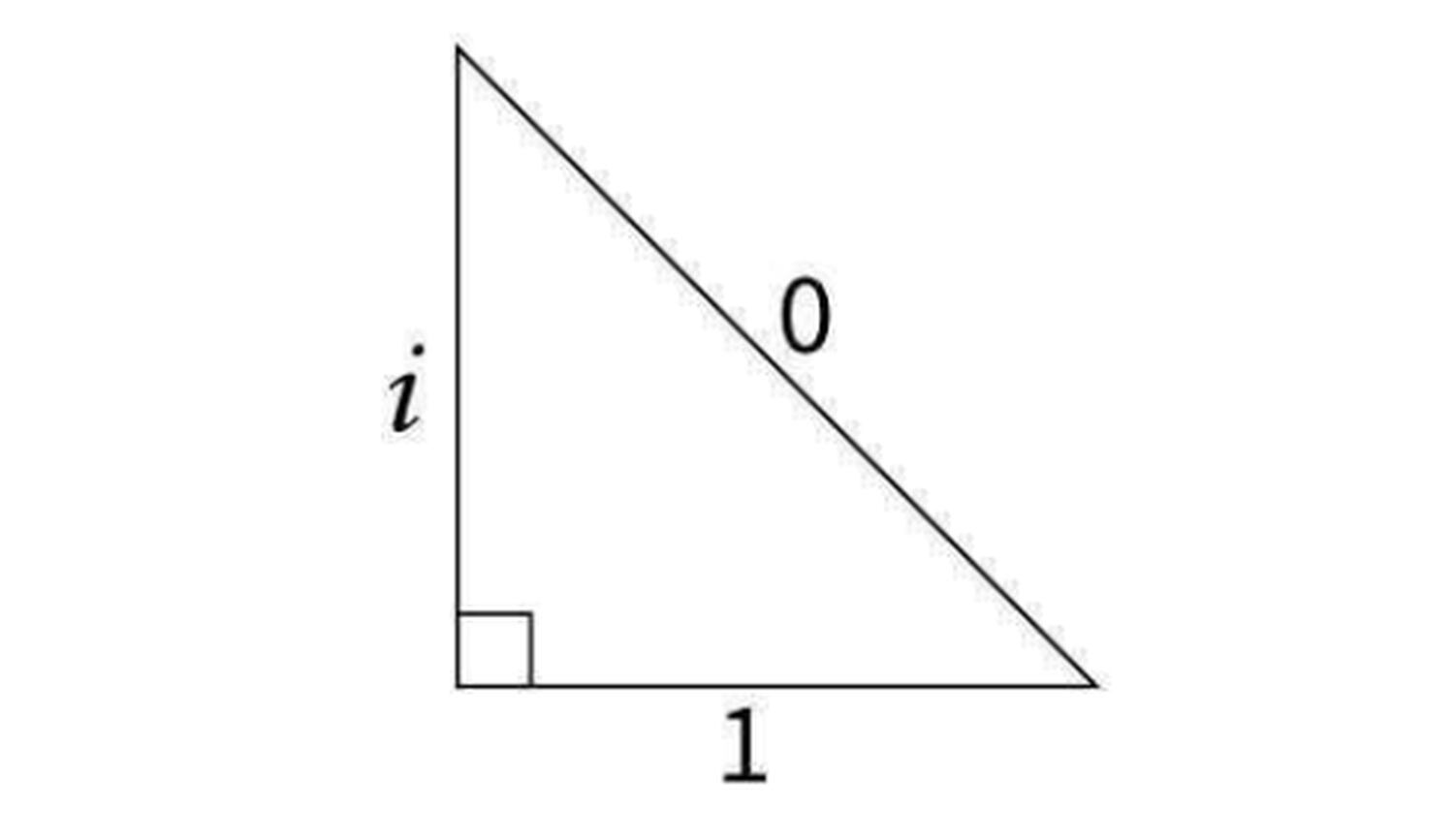
Por el teorema de Pitágoras, i al cuadrado + 1 al cuadrado = -1 + 1 = 0. ¿Qué puedes decir al respecto?
Y, por último, en nuestra relación de rectángulos singulares falta uno, ¿cuál es?
Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos Maldita física, Malditas matemáticas o El gran juego. Fue guionista de La bola de cristal.
Fuente:https://elpais.com/ciencia/2020-04-17/rectangulos-singulares.html


Sé el primero en comentar en «Rectángulos singulares»