Aunque la criptografía es el arte de comunicar de manera secreta, también podríamos decir que es la ciencia de los desafíos. Así, la idea principal para transmitir información de forma segura por internet es que podemos probar que somos quienes decimos ser, resolviendo un reto.

Por ejemplo, para acceder al correo o redes sociales usamos contraseñas. Si alguien quiere entrar a nuestra cuenta, su desafío consiste en averiguar la clave. Si esta es suficientemente complicada, averiguarla debería ser tan difícil como encontrar una aguja en un pajar.

En matemáticas, un grupo es un conjunto con una operación asociativa. Los números enteros {…,-3,-2,-1,0,1,2,..} con la operación de sumar, son un grupo. Las fracciones (sin el cero) con la multiplicación forman otro grupo. La estructura de grupo puede aparecer de formas muy curiosas e inesperadas. Por ejemplo, para cada número natural n, hay un grupo llamado grupo de trenzas en n cuerdas cuyos elementos son dibujos como el de abajo (aquí hemos tomado n = 4)

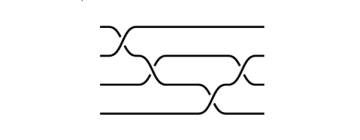
Cada dibujo representa un elemento del grupo de trenzas (podemos pensar que cada dibujo es un número). Pero hay que tener en cuenta que en una trenza se pueden deslizar los cruces en las cuerdas, y sigue siendo la misma trenza, por lo que dibujos diferentes representan el mismo elemento. Por ejemplo, los siguientes pares de dibujos representan al mismo grupo de cuatro cuerdas.

 La operación entre las trenzas es de lo más sencillo. Unimos el final de las cuerdas de un dibujo con el principio de las cuerdas de otro dibujo para obtener una nueva trenza. Usamos +para denotar la operación. Aquí un ejemplo.

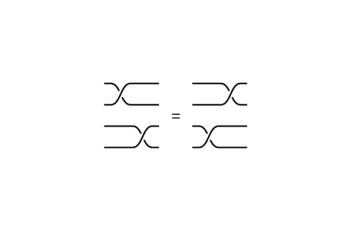
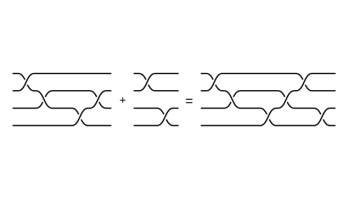 Para que sea un grupo ha de cumplir ciertas propiedades. Primero, debe haber un elemento especial, que es neutro, que al operarlo con cualquier elemento, lo deja como estaba. El cero es el neutro para la suma de números, y el 1 lo es para la multiplicación de fracciones. En el caso de las trenzas de n cuerdas, el elemento neutro es el dibujo de n cuerdas sin trenzar. La segunda propiedad es la existencia de inversos. Al operar un elemento con su inverso, se obtiene el neutro. El inverso de 3 respecto la suma es -3, y de 4, respecto a la multiplicación, es ¼. En nuestro caso, el inverso consiste en “desenredar” las cuerdas. Por ejemplo, con tres cuerdas, si tenemos la trenza en la que la cuerda 2 pasa sobre la cuerda 3, su inverso será la trenza que pasa la cuerda 3 sobre la cuerda 2. Su unimos estos dos dibujos y estiramos de los extremos, obtenemos tres cuerdas sin trenzar.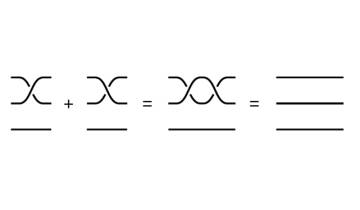

 Ahora que ya sabemos que es un grupo, podemos usarlo para plantear ecuaciones y usarlas como desafíos criptográficos. Las primeras propuestas para aplicar las trenzas a la criptografía datan de 1999 y 2000 y el desafío para conseguir seguridad se basaba en resolver la llamada ecuación de conjugación, que tiene forma a + x = x + b dónde a y b son trenzas conocidas y x es una trenza incógnita. Sin embargo, durante los años 2000 varios equipos de matemáticos encontraron algoritmos (1, 2, 3) para resolver esta ecuación y finalmente esas propuestas fueron desechadas.

Ahora el algoritmo WalnutDSA las recupera para la firma digital. Para que alguien falsifique una firma debería ser capaz de resolver ecuaciones que combinan matrices y trenzas, lo que es un reto muy complicado, no solo para los ordenadores actuales sino también, según afirman los autores del protocolo, para ordenadores cuánticos.

Además del grupo de trenzas, existen otros grupos interesantes en los que plantear criptosistemas. Un ejemplo popular es el de los grupos policíclicos o los graph groups en los que es fácil codificar problemas de grafos. La idea es siempre la misma: si encuentras un desafío que los matemáticos no son capaces de resolver de forma eficiente, puede ser que hayas topado con un diamante para la criptografía.

Fuente:https://elpais.com/elpais/2019/05/06/ciencia/1557136645_167329.html