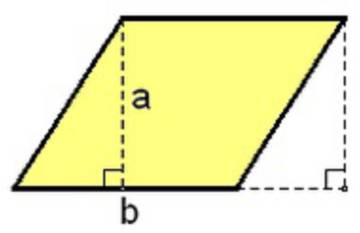
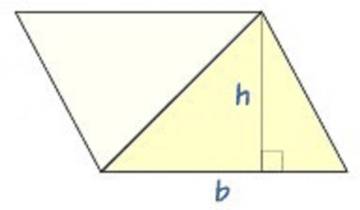
La única figura geométrica cuya fórmula del área es evidente, es el rectángulo, pues no hay más que multiplicar la longitud de la base por la de la altura para hallar el número de unidades cuadradas. Por ejemplo, si tenemos un rectángulo de 5 centímetros de base y 3 de altura, es evidente que contendrá 5 x 3 = 15 cuadraditos de 1 centímetro de lado, o sea 15 centímetros cuadrados. Generalizando, la superficie (S) de un rectángulo de base b y altura a será S = b.a.

 Es fácil ver que cualquier paralelogramo se puede convertir en un rectángulo “cortando” un triángulo rectángulo de un extremo y “pegándolo” en el otro, por lo que también en este caso el área se obtendrá multiplicando la base por la altura: S = b.a.

 Y puesto que cualquier triángulo puede considerarse la mitad de un paralelogramo de igual base y altura (que podemos obtener trazando por dos de los vértices sendas paralelas a los lados opuestos, como muestra la figura), el área de un triángulo será b.h/2 (la altura suele designarse indistintamente con las letras a o h).

 En el caso de un polígono regular, como el hexágono de la figura, que tiene todos sus lados y todos sus ángulos iguales, podemos dividirlo, trazando sus radios, en tantos triángulos isósceles iguales (que en el caso del hexágono serán equiláteros) como lados tiene. Por lo tanto, su área será n.l.a/2, siento n el número de lados, l el lado del polígono y a la altura de cada triángulo, que es la apotema del polígono; pero n.l es el perímetro (p) del polígono, luego su área será p.a/2.

Para hallar el valor de π, Arquímedes imaginó un círculo encerrado entre un polígono inscrito y uno circunscrito de un número de lados cada vez mayor. Obviamente, la longitud de la circunferencia tenía que ser siempre mayor que el perímetro del polígono inscrito y menor que el perímetro del polígono circunscrito, y a partir de sendos polígonos de 96 lados respectivamente inscrito y circunscrito, halló un valor de π comprendido entre las fracciones 223/71 y 22/7; la media de estos dos valores es aproximadamente 3,1418, lo que significa que en el valor hallado por Arquímedes el error es de apenas dos diezmilésimas.

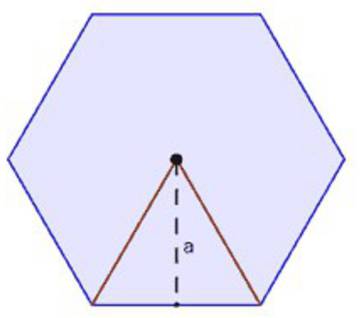
Y aunque el razonamiento mediante el cual el gran matemático griego llega a la fórmula del área del círculo es algo más largo y elaborado, en última instancia equivale a considerar que el círculo es un polígono regular de infinitos lados infinitamente pequeños, por lo que su apotema es el radio del círculo y su perímetro la longitud de la circunferencia, con lo que la fórmula p.a/2 se convierte en 2πr.r/2 = πr².

Es curiosa la forma en que Arquímedes presenta el área del círculo, diciendo que es igual a la de un triángulo rectángulo cuyos catetos son, respectivamente, el radio del círculo y la longitud de su circunferencia. Un guiño al viejo problema de la cuadratura del círculo, aunque seguramente Arquímedes ya sabía que era irresoluble. Pero esa es otra cuestión…

Fuente:https://elpais.com/elpais/2019/03/04/ciencia/1551686906_351630.html